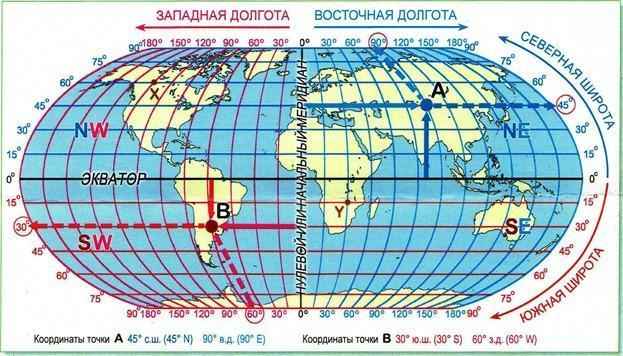
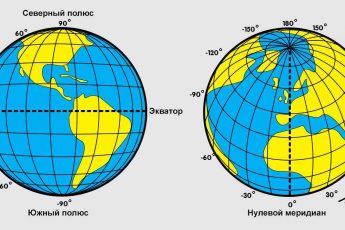
С помощью карты можно определять расстояние между точками на земной поверхности, но точность таких вычислений невысока.
Ситуация относительно проста, если точки лежат на одном меридиане. Все меридианы имеют одинаковую длину. Можно подсчитать, что одному градусу широты соответствует примерно 111,3 км реальной длины. Поэтому надо найти разницу в долготе между точками и умножить ее на 111,3 км. Например, если точка А находится на северной широте 50°, а Б располагается на северной широте 32°, и при этом у них совпадает долгота, то расстояние между ними составит.
111,3х(50° – 32°) = 111,3х16 = 1780,8 км
Ситуация меняется, когда одна точка имеет северную, а другая – южную широту. В этом случае широты уже надо складывать. Так, если бы точка Б из предыдущего примера располагалась бы на южной широте 32°, то расстояние от А до Б составило бы:
111,3х(50° + 32°) = 111,3х82 = 9126,6 км
Ситуация усложняется, когда точки находятся на разных меридианах, но на одной параллели. Если у обеих точек долгота западная (или, наоборот, восточная), то сначала надо найти разницу их долгот. Если же одна точка имеет восточную, а другая западную долготу, то их надо суммировать. Далее результат надо умножить на длину 1° параллели. Эта длина у параллелей различна и зависит от их широты. Можно воспользоваться таблицей ниже:
| Широта параллели | Длина ее дуги величиной в 1° |
|---|---|
| 0° | 111,3 |
| 5° | 110,9 |
| 10° | 109,6 |
| 15° | 107,6 |
| 20° | 104,6 |
| 25° | 102,1 |
| 30° | 96,5 |
| 35° | 91,3 |
| 40° | 85,4 |
| 45° | 78,8 |
| 50° | 71,7 |
| 55° | 64,0 |
| 60° | 55,8 |
| 65° | 47,2 |
| 70° | 38,2 |
| 75° | 28,9 |
| 80° | 19,4 |
| 85° | 9,7 |
| 90° | 0 |
Например, нужно найти расстояние между точками, имеющими координаты:
А – 60° с. ш, 39° з. д.
Б – 60° с. ш, 25° з. д.
Широты у них одинаковы, поэтому смотрим на долготу. Она у обеих точек западная, поэтому надо найти их разницу:
39° – 25° = 14°
Полученный результат надо умножить на длину 1° параллели, широта которой составляет 60°. По табличке определяем, что на широте 60° дуга в 1° имеет длину 55,8 км. Перемножаем два числа:
14°х 55,8 км = 781,2 км
Список использованных источников
• https://www.yaklass.ru/p/geografiya/5-klass/izobrazheniia-zemnoi-poverkhnosti-i-ikh-ispolzovanie-131512/geograficheskie-koordinaty-161116/re-d77ff3cc-0858-4fd8-aabd-69f1fdffb41d • https://interneturok.ru/lesson/geografy/5-klass/plan-i-karta/gradusnaya-setka-geograficheskaya-dolgota-i-shirota